Soft Subdivision Search
-
Advised by: Prof. Chee Yap
- Exact Approach: This approach can theoretically solve any algebraic planning problem. However, in practice, exact algorithms are often implemented using machine approximations, which undermines their guarantees. As a result, "exact" algorithms are generally impractical except for the simplest cases.
- Sampling Approach: Dominant in motion planning research over the past two decades, this approach is best represented by the Probabilistic Road Map (PRM). Its primary limitation is the inability to handle termination effectively, commonly known as the "narrow passage problem."
- Subdivision Approach (Cell Decomposition): The oldest of the three, this approach remains popular among practitioners and is the foundation of our work. We introduced the concept of resolution-exactness as a theoretical basis for path planning that avoids exact computation. This innovation enables the use of soft predicates, which replace traditional predicates that govern the logic of geometric algorithms. For more information about our work, please visit the NYU Exact Geometric Computation group (EGC).
Date: Sep. 2015 - July 2017
Motion planning is a fundamental problem in robotics, with three primary approaches:
Path Planning for Simple Robots using Soft Subdivision Search
We introduce the Soft Subdivision Search (SSS) framework, a novel approach for designing path planning algorithms grounded in the concept of resolution-exactness. This video demonstrates the SSS framework applied to three simple planar robots: a disc, a triangle, and a 2-link robot. The algorithm achieves state-of-the-art real-time performance and is both computationally efficient and straightforward to implement.
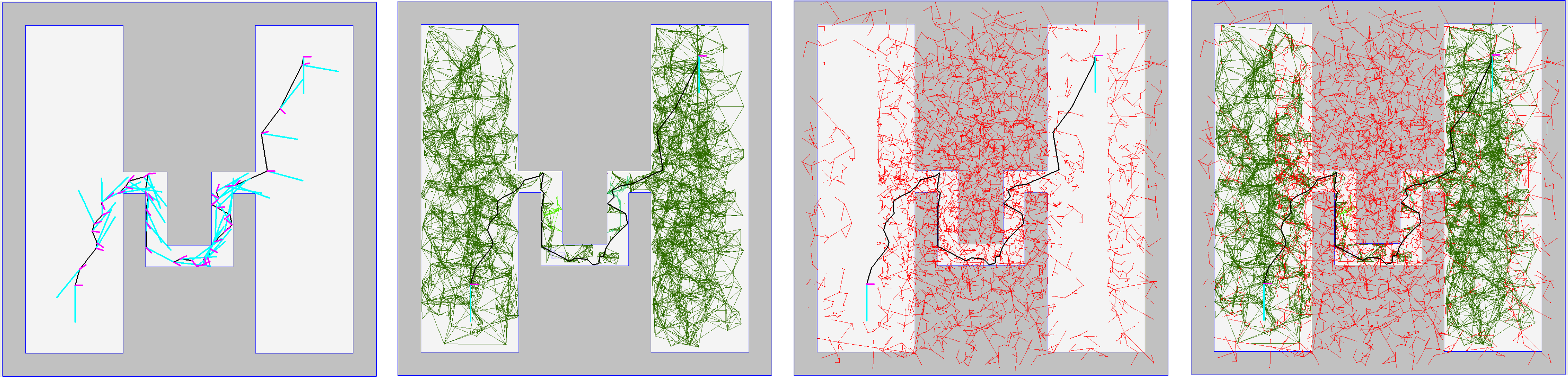
Resolution-Exact Planner for Thick Non-Crossing 2-Link Robots
We propose a novel and efficient planner for non-crossing 2-link thick robots, contributing to the development of practical and theoretically sound subdivision planners. While it is commonly assumed that resolution-exact approaches trade stronger theoretical guarantees for slower runtime compared to sampling-based methods, our experiments challenge this notion. The results indicate that our Soft Subdivision Search (SSS) framework consistently outperforms sampling approaches in both speed and success rate.
For performance comparison, we utilized sampling-based approaches from the Open Motion Planning Library (OMPL) and implemented one of the latest PRM variants, Lazy Toggle PRM. To ensure fairness, we adopted open-source libraries as the primary benchmark but also implemented PRM and RRT algorithms independently. For further illustration, please refer to our RRT demonstration video, which showcases a 2-link robot navigating with different step sizes.
Rods and Rings: Soft Subdivision Planner for R³ x S²
We continue advancing the Soft Subdivision Search (SSS) framework for rods and rings in 3D, now with practical implementations. A key technical shift from our prior work on planar robots is abandoning the notion of "forbidden orientations," which becomes exceedingly complex for spatial robots. Instead, we adopt an alternative strategy by introducing Σ2-sets to bound the footprints of boxes. These sets generalize the concept of Π1-sets from our earlier work, providing greater flexibility and enabling the extension of planners to "thick" rods and rings. While this approach entails a modest increase in the accuracy constant K, it significantly enhances the robustness and adaptability of our algorithms.
Ching-Hsiang Hsu, Yi-Jen Chiang, and Chee Yap, "Soft Subdivision Planner for a Rod," Fall Workshops on Computational Geometry, New York, NY, Oct 27-28, 2016.
Ching-Hsiang Hsu, Yi-Jen Chiang, and Chee Yap, "Rods and Rings: Soft Subdivision Planner for R³ x S²," Proc. 35th International Symposium on Computational Geometry (SoCG), Portland, OR. June 18-21, 2019.
There is no royal road to geometry. - Euclid


